Shell Normalization Against Angled Armor in War Thunder

In War Thunder, when a shell collides with an armor plate, a modifier will be applied to the thickness of the plate depending on the angle of impact and the type of shell. This is how War Thunder models a phenomenon known as normalization.

Overview of Normalization

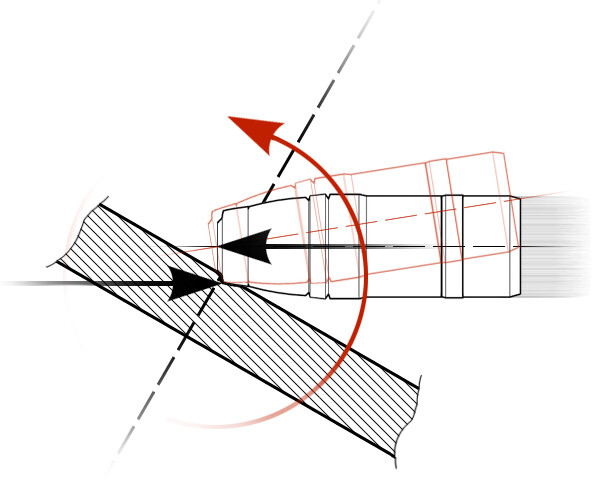
Normalization is the effect of a shell curving into the plate to penetrate it at a flatter angle. Overly simplified, if a shell with 5° of normalization impacts a plate at an angle of 30°, then the shell will only have to deal with the line of sight (LoS) thickness of the plate at 25°. However, if that shell also denormalizes by 7° at that impact angle against that plate, it will have to penetrate a LoS thickness of 32°.

Shells with certain characteristics normalize more than other shells. For example, shells with flat noses normalize a lot, shells with large caliber tend to normalize more, and shells with caps normalize more than equivalent shells without caps. Russian flat-nose projectiles don’t explicitly state they are flat-nosed in game, but they often just display as APHEBC, the ballistic cap covering the flat nose of the projectile. Chemical shells (HE, HEAT) do not normalize at all, except for HESH, which could be argued to have infinite normalization, though through different means.

Effects of Normalization in War Thunder

Line of Sight thickness (LoS) is calculated by finding how thick an armor plate is at a given angle. For example, at 60° an armor plate doubles its line of sight thickness, meaning a 100mm plate at 60° is equivalent to a 200mm plate at 0°.

Throughout the article, the “LoS equivalent” means that the amount of protection provided against that shell at that angle is equal to the LoS thickness at the angle specified. For example, a shell hitting at 50° but only having to go through what would be equal to LoS thickness of 45° against that plate, has a LoS equivalent of 45° since it normalized by 5°. It can also be thought of as the HEAT protection equivalent, since they are the same. You will need to understand this to understand the article.

To find LoS thickness quickly, use a HEAT shell’s Equivalent protection value, as they don’t normalize and the value will always be equal to the LoS thickness at the observed angle against that plate.

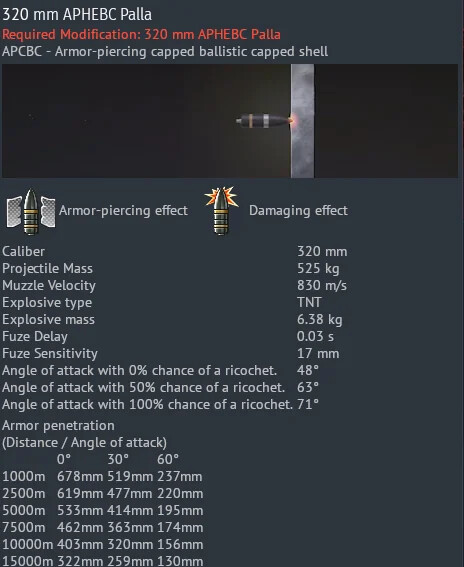
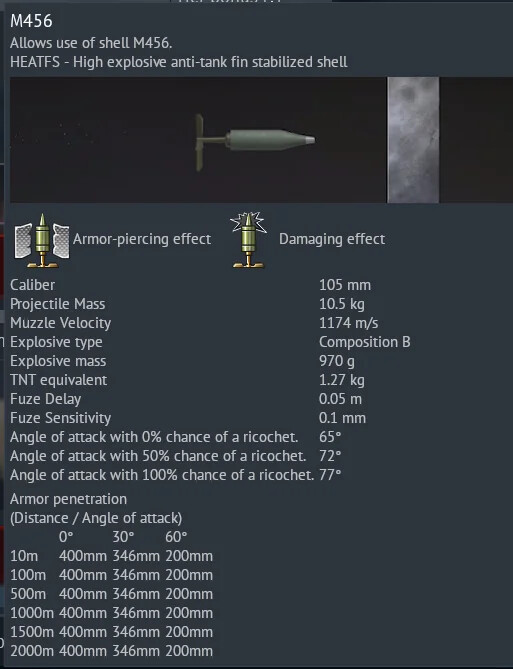
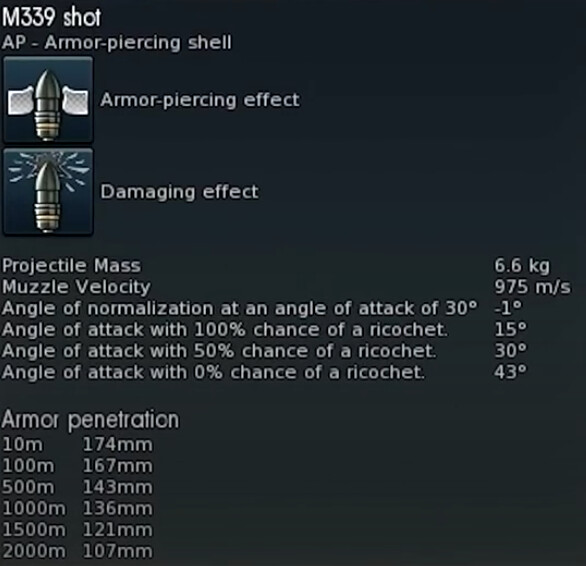
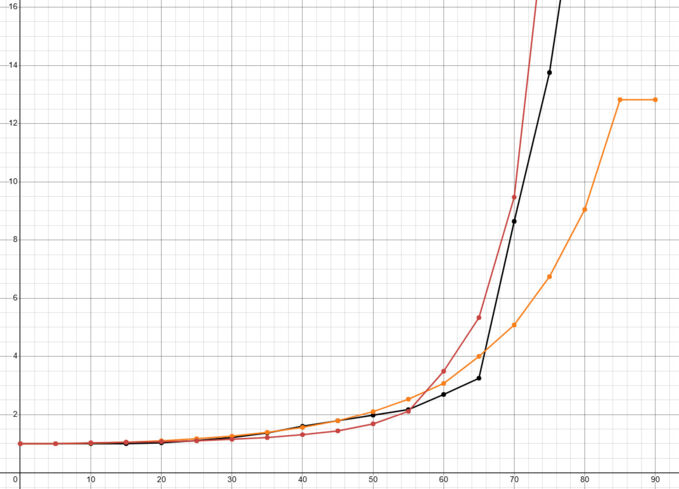
A very drastic example of normalization and denormalization can be found by using the ISU-152's cannon against the Jagdtiger’s 80mm side plate.

As we can see from these examples, the difference in normalization of the normal APHE shell and the flat-nose shell was 13°, which makes for some rather drastic effects in the amount of armor that must be penetrated.

The Holy Stat Card

The stat cards for shells in War Thunder should be interpreted as follows:

1. The actual penetration of the shell at a given range is the value listed at 0°
2. The penetration at 30° and 60° are how thick of a plate the shell can penetrate at that angle (not LoS thickness).
3. Caliber:Plate thickness ratio is automatically accounted for by the stat card, so there is no need to worry about the caliber of the gun affecting it.

So as seen, at 5000m the shell has 533mm of pen, so if it hit a plate at 30°, the thickest plate it could overcome at that angle is 414mm thick (Not LoS). So if this shell hit a 320mm plate at 30° at 10km, it would theoretically penetrate exactly.    (The card automatically calculated the 1:1 ratio for this situation)

This can be used to relatively compare shells' performance levels at 30° and 60° angles.

This is why HEAT shells always display half the 0° penetration at 60°, they are still going through the actual amount of armor the 0° figure states, but the thickest plate they can pen at 60° is equal to half because of the LoS thickness multiplier.

Ricochets and Normalization

There are two separate normalization mechanics in War Thunder, one which affects the penetration of the shell, which is the main one discussed in this article, called the Slope Modifier. The second one affects how much the shell’s ricochet angles are affected upon impact of a plate, which will be discussed only here.

In the files, the modifiers are all over the place. Just know that a shell can decide to normalize against armor and not ricochet when it otherwise should have. It is also linked to caliber to plate thickness ratio, and APC and APCBC seem to normalize slightly better than other shells. This type of normalization only affects ricochet angle.

Fun fact: This use to be shown on the stat card once upon a time (9 years ago).

Denormalization

Denormalization can be thought of as negative normalization, the shell curving away from the plate, which is generically displayed in the animation shell card.

Once again, denormalization does not actually affect the flight path of the shell in game, it is simply based on the modifier that is applied to the thickness of the plate.

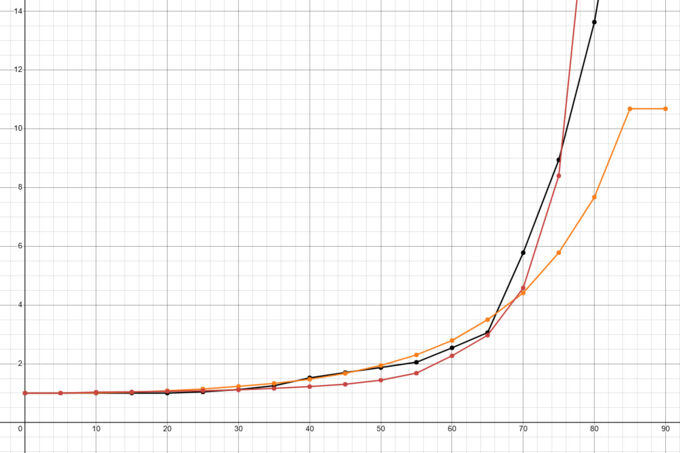
As we can see this time, at the same angle, against a plate 150mm thick instead of 80mm thick from earlier, the normalization angles dropped. The difference in normalization between the flat-nosed and normal shell was only 2.5° instead of 13° and the difference in penetration was 23mm instead of 41mm as seen in the 80mm plate test.

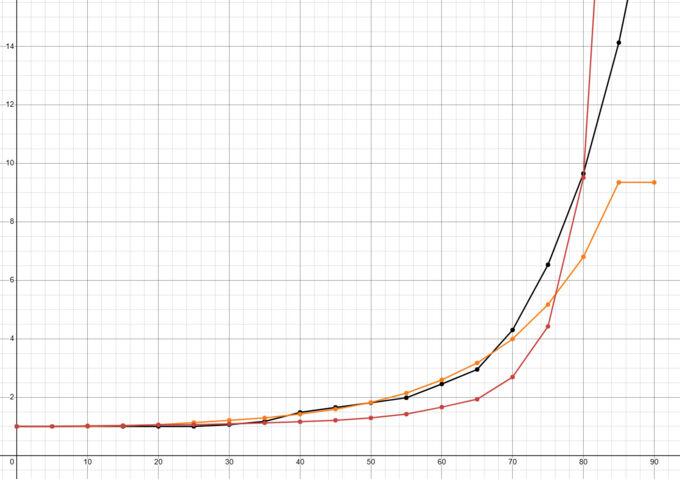
This shows the relationship between caliber to plate thickness when it comes to the normalization rate. When the shell is about 2:1 it normalizes much more than it does when the ratio is at about 1:1. Here are some more examples:

Normalization in the Code

In the code, the modifier for normalization is calculated as a multiplier to the plate thickness/protection. It has nothing to do with reducing angles by a given percent at all. (Though that is what its simulating in addition to LoS thickness.)

Note that for these calculations, plate thickness is measured in RHA equivalent. For example, 100mm of structural steel would be calculated for as if a 45mm plate of RHA. Shell caliber is calculated on the size of the penetrating warhead, so for subcaliber rounds like APCR or APDS, it will not be equivalent to the caliber of the gun, but the caliber of the penetrating body, which is unfortunately not listed in game.

Also note that the modifiers will never drop below the values of 0.5:1 or exceed the values of 2.5:1 regardless of the actual ratio, except for overmatch, when the ratio is 7:1 or greater and the thickness multiplier is always 1 regardless of angle.

However, multiplier values between the caliber to plate thickness ratios of 0.5:1 and 2.5:1 will smoothly transition between multipliers, they won’t suddenly jump when they hit a certain threshold.

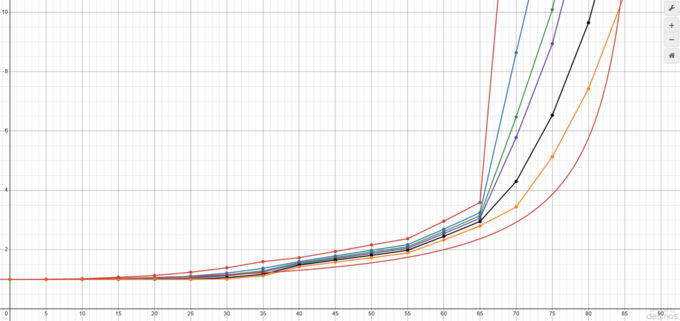
As we can see, the modifiers don’t follow a smooth exponential curve that we would expect, instead having multiple jagged linear strips, primarily between 40° and 55°, and between 55° and 65°. I don’t know how they calculated these modifiers, however I made a spreadsheet with them listed that is linked later.

We can see that the difference between shell types at 1:1, especially AP and the other shells isn’t as wide as you would expect. AP even outperforms in some areas (though it’s important to remember non-capped AP has poor ricochet angles). APBC rounds outperform in most reasonable areas, except for 60-65° in which APC does better. Values at angles past 70° don’t really matter as much because you will likely ricochet or non-pen due to the ridiculously high modifiers.

APBC performance increases faster than other shell types at higher Caliber:Plate thickness ratios, so large caliber guns benefit highly from the APBC modifier. Note that AP modifiers are for non-capped AP shells, APC modifiers are for APC or APCBC rounds, and the APBC modifier is for flat-nosed APBC rounds only. This excludes APBC rounds like the M103's APBC round, which uses the AP modifier because it is not a flat-nose round. Info on this can also be found in the spreadsheet I made linked later in this section.

To use the calculators, you must make a copy of the document to edit the calculator input fields. File > Make A Copy

Closing Thoughts

Remember to look at the characteristics of your shells in the protection analysis and run them through a couple scenarios to see what shell you should bring, especially for Russian machines as they may have a flat-nosed shell that makes the lesser penetration worth it. (The one exception being the 122mm gun, where I find the D variant better than the flat-nosed B variant in general performance against the targets you face.)

Additionally, this article mainly focuses on full-caliber shells. Generally, APDS has good normalization, and APFSDS tends to have excellent normalization. APCR, as previously stated, has the worst normalization characteristics in the game. I added the modifiers of modern shells to the spreadsheet as well. Many of them don’t make use of caliber:plate thickness ratio, so the subcaliber doesn’t matter as much as it would typically.

Happy hunting tankers!